Funktionenschar h
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Flächenstück
Mit
\(\quad \begin{array}{ r c l } f_a(t) & = & h_a(t) \end{array} \)
\(\\\)
wird der Schnittpunkt der Graphen berechnet. \(t_0\) ist der \(t\)-Wert im Intervall \([1;2]\), wo sich die Graphen schneiden.
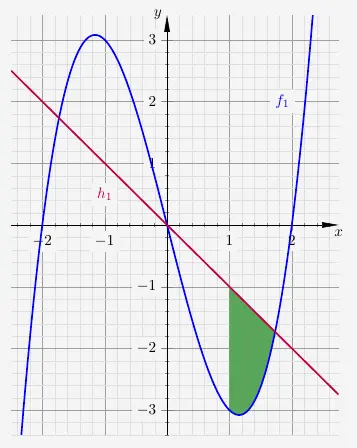
\(\\[2em]\)
Aufgabe 2 – Berechnung des Terms
Wir berechnen die Schnittstellen.
\( \quad \begin{array}{ r c l l } h_a(t) & = & f_a(t) \\[6pt] -a \cdot t & = & a \cdot \left(t^3 - 4 t\right) & | + a \cdot t \\[6pt] 0 & = & a \cdot \left(t^3 - 4 t\right) + a \cdot t \\[6pt] 0 & = & a \cdot \left(t^3 - 4 t + t \right) \\[6pt] 0 & = & a \cdot \left(t^3 - 3 t \right) \\[6pt] 0 & = & a \cdot t \cdot \left( t^2 - 3 \right) \\ \end{array} \)
\(\\\)
Mit dem Nullprodukt erhalten wir die Lösung \(a = 0\), \(t = 0\) und \(t^2 - 3 = 0\). Da \(a\) stets positiv ist und \(t_0\) im Intervall \([1;2]\) liegt, bleibt nur der Lösungsansatz \(t^2 - 3 = 0\).
\(\\\)
\( \quad \begin{array}{ r c l l } t^2 - 3 & = & 0 & | +3 \\[6pt] t^2 & = & 3 & | \sqrt{\dots} \\[6pt] t_1 & = & \sqrt{3} \\[6pt] t_2 & = & -\sqrt{3} \\ \end{array} \)
\(\\\)
\(t_1 = \sqrt{3} \approx 1{,}732\) ist die einzige Lösung im Intervall \([1;2]\) und stellt den Wert von \(t_0\) dar.
Weiter berechnen wir die Fläche im Intervall \([1;\sqrt{3}]\) für alle \(a>0\).
\(\\\)
\( \quad \begin{array}{ r c l l } A(a) & = & \begin{array}{ r c l } \begin{vmatrix} \displaystyle{\int}_1^{\sqrt{3}} f_a(t) dt \end{vmatrix} \; - \; \begin{vmatrix} \displaystyle{\int}_1^{\sqrt{3}} h_a(t) dt \end{vmatrix} \\ \end{array} \\[15pt] & = & \begin{array}{ r c l } \begin{vmatrix} \displaystyle{\int}_1^{\sqrt{3}} \left(a t^3 - 4a t \right) dt \end{vmatrix} \; - \; \begin{vmatrix} \displaystyle{\int}_1^{\sqrt{3}} (-a t) dt \end{vmatrix} \\ \end{array} \\[15pt] & = & \begin{array}{ r c l } \begin{vmatrix} \Big[ \frac{1}{4}a t^4 - 2a t^2 \Big]_1^{\sqrt{3}} \end{vmatrix} \; - \; \begin{vmatrix} \Big[ -\frac{1}{2}a t^2 \Big]_1^{\sqrt{3}} \end{vmatrix} \\ \end{array} \\[15pt] & = & \begin{array}{ r c l } \begin{vmatrix} \frac{1}{4}a \left(\sqrt{3}\right)^4 - 2a \left(\sqrt{3}\right)^2 -\left(\frac{1}{4}a \cdot 1^4 - 2a \cdot 1^2\right) \end{vmatrix} \; - \; \begin{vmatrix} \left( -\frac{1}{2}a \left(\sqrt{3}\right)^2 - \big(-\frac{1}{2}a \cdot 1^2\big) \right) \end{vmatrix} \\ \end{array} \\[12pt] & = & \begin{array}{ r c l } \begin{vmatrix} \frac{9}{4}a - 6 a -\left(\frac{1}{4}a - 2a \right) \end{vmatrix} \; - \; \begin{vmatrix} \Big( -\frac{3}{2}a - \big(-\frac{1}{2}a \big) \Big) \end{vmatrix} \\ \end{array} \\[12pt] & = & \begin{array}{ r c l } \begin{vmatrix} \frac{9}{4}a - 6 a - \frac{1}{4}a + 2a \end{vmatrix} \; - \; \begin{vmatrix} \left( -\frac{3}{2}a + \frac{1}{2}a \right) \end{vmatrix} \\ \end{array} \\[12pt] & = & \begin{array}{ r c l } \begin{vmatrix} 2a - 6 a + 2a \end{vmatrix} \; - \; \begin{vmatrix} -a \end{vmatrix} \\ \end{array} \\[8pt] & = & | -2a | - a \\[6pt] & = & a \\ \end{array} \)
\(\\\)